Answer:

Step-by-step explanation:
To find the number of baseballs that can fit in the container, we need to calculate the volume of both the baseball box and the shipping container. Then, we can divide the volume of the container by the volume of a single baseball box to determine the number of baseballs.
Let's start with the volume of the baseball box. Since it is a cube, all sides have the same length of 5x units. To calculate the volume, we need to multiply the length, width, and height of the cube. In this case, it would be:
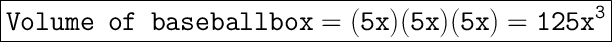
Now let's move on to the volume of the shipping container. It is also a cube with sides measuring 10x⁴ units. So, the volume of the container would be:
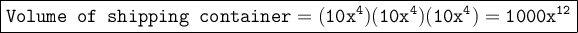
To find out how many baseballs can fit in the container, we divide the volume of the container by the volume of a single baseball box:
Therefore, the simplified form of the answer is 8x^9. This means that 8x^9 baseballs can fit in the shipping container.
#BTH1
________________________________________________________