Answer:
122.50 feet
Explanation:
First, recall
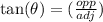 , where opp is the leg of the right triangle representing the height of the tree and adj represents the leg of the right triangle representing the distance from the tree. For this problem, let
, where opp is the leg of the right triangle representing the height of the tree and adj represents the leg of the right triangle representing the distance from the tree. For this problem, let
Θ= 54°
adj = 89 ft.
So,
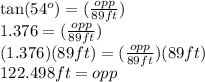
For this problem, remember the opposite side represents the height of the tree. So, the height of the tree, rounded to the nearest hundredth, is 122.50 feet.