Question

Use “like bases” to solve

Answer 1

Write 9 = 3² and 27 = 3³, then 1/9 = 3⁻² and 1/27 = 3⁻³.

So, we have

`\left(\frac1{27}\right)^(2x+1) = \left(\frac19\right)^(x+4)`

`\left(3^(-3)\right)^(2x+1) = \left(3^(-2)\right)^(x+4)`

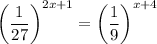
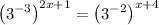
Recall that
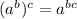`(a^b)^c = a^(bc)` for real a, b, and c. Then this equation is the same as

`3^(-3(2x+1)) = 3^(-2(x+4))`

`3^(-6x - 3) = 3^(-2x - 8)`

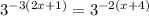
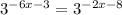
The bases on either side are the same, so the exponents must be equal:

-6x - 3 = -2x - 8

Solve for x :

-4x = -5

x = 5/4