Question

A 240 N force is pulling a 85.0 kg refrigerator across a horizontal surface. The force acts at an angle of 20 above the surface. The coefficient of kinetic friction is 0.200, and the refrigerator moves a distance of 8.00 m. Calculate the work done by the kinetic friction force.

Answer 1

Approximately
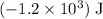`(-1.2* 10^(3))\; {\rm J}` (assuming that
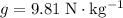`g = 9.81\; {\rm N \cdot kg^(-1)}` and that the refrigerator moved along a straight line.)

Step-by-step explanation:

It is given that the fridge is on a level surface. The following forces would act on the fridge in the vertical direction:

• Weight of the fridge (downwards.)
• Normal force from the ground (upwards.)
• Vertical component of the force pulling on the fridge (upwards.)

Weight of the refrigerator:

`(\text{weight}) = m\, g = (85.0\; {\rm kg})\, (9.81\; {\rm N \cdot kg^(-1)}) = 833.85\; {\rm N}`.

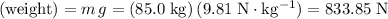Let
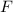`F` denote the force pulling on the fridge. Let
`\theta` denote the angle of elevation of this force. It is given that
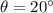`\theta = 20^(\circ)`. The vertical component of this force will be:

`\begin{aligned}F\, \sin(\theta) &= (240\; {\rm N})\, \sin(20^(\circ)) \approx 82.085\; {\rm N}\end{aligned}`.

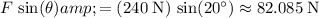Since the fridge isn't moving in the vertical direction, the resultant force on the fridge in that direction should be
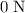`0\; {\rm N}`. Thus:

`\begin{aligned} & (- (\text{weight})) + (\text{normal force}) + F\, \sin(\theta) = 0\; {\rm N} \end{aligned}`.

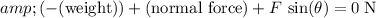Rearrange this equation to find
`(\text{normal force})`.

`\begin{aligned} (\text{normal force}) &= (\text{weight}) - (\text{normal}) \\ &\approx (833.85\; {\rm N}) - (82.805\; {\rm N}) \\ &\approx 751.77\; {\rm N}\end{aligned}`.

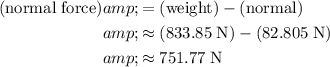The kinetic friction on this fridge would be:

`\begin{aligned}& (\text{kinetic friction}) \\ =\; & (\text{coefficient of kinetic friction}) \, (\text{normal force}) \\ \approx\; & (0.200)\, (751.77\; {\rm N}) \\ \approx\; & 150.35\; {\rm N}\end{aligned}`.

Note that the displacement of the refrigerator is opposite to the direction to the direction of the kinetic friction. Thus,
`(\text{displacement}) = (-8.00\; {\rm m})`.

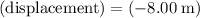Multiply kinetic friction by displacement to find the work done:

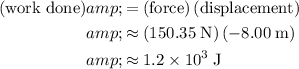`\begin{aligned}(\text{work done}) &= (\text{force})\, (\text{displacement}) \\ &\approx (150.35\; {\rm N})\, (-8.00\; {\rm m}) \\ &\approx 1.2 * 10^(3)\; {\rm J}\end{aligned}`.