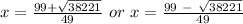Question

Please help on this question :) tyyy

Answer 1

`\mathrm{x_1=99/49-\sqrt38221/49;x_2=99/49+\sqrt38221/49}\\`

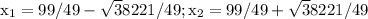
Explanation:

Analyze the function:

f(x)=
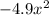`-4.9x^(2)`+19.8x+58

To find the x-intercept, set y=0:

`-4.9x^(2)` +
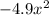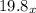`19.8_(x)` + 58 = 0

Convert decimal to fraction:

`-(49)/(10)x^(2)` +
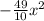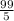`(99)/(5)`x+58=0

Reduce the fraction:

`-(49)/(10)`
`x^(2)` +
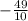
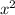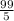`(99)/(5)` x + 58 = 0

Multiply both sides of the equation by the common denominator:

`-(49x10)/(10)`×
`x^(2)`+
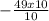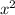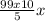`(99x10)/(5) x` × + 58 × 10 = 0 × 10

Reduce the fractions:

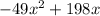`-49x^(2)+198x` + 58 × 10 = 0 × 10

Calculate the product or quotient:

-49
`x^(2)+198x+580=0`

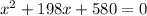
Make the leading coefficient positive:

49
`x^(2) -198x-580=0`

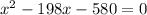
Identify the coefficients:

a = 49, b = -198, c = -580

Substitute into x =
`(-b\pm√(b^2-4ac))/(2a)`

`x=\frac{-\left(-198\right)+\sqrt{{(-198)}^2-4*49*(-580)}}{2*49}\\`

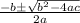
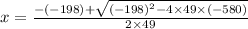
or

`x=\frac{-(-198)-\sqrt{{(-198)}^2-4*49*(-580)}}{2*49}`

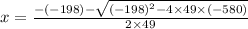
Combine the results:

`x=(99+√(38221))/(49)\ or\ x=(99\ -\ √(38221))/(49)\\\\`