Question

8 A circle passes through the points (0, 2) and (0,8) and its centre lies on the line

x=4.
Draw a sketch and find the equation of the circle.

Answer 1

Explanation:

A circle that passes through point 0,2 and (0,8) and has a center that lies on x=4 is what given.

So we know is center (4,p) for some number p,

Since the points on circumference of the circle have the same x value, then we know that the y coordinate of the center must be the midpoint of the circumferences' y coordinates.

Why?

A circle is not a function since it doesn't pass the vertical line test. And the standard form of a circle is

`{x}^(2) + {y}^(2) = {r}^(2)`

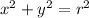
With center (0,0).

Consider the equation

`{x}^(2) + {y}^(2) = 9`

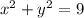
The radius is 3 so two points with x coordinate 0 is

(0,3) and (0,-3). And the midpoint of them is (0,0) which is the center. Which is the defining trait of all circles.

Now, back on hand, our the midpoint of 2 and 8 is 5 so our center is

(4,5).

Now, we must find the radius. We use distance formula.

For (4,5) and (0,8).

`d = \sqrt{(8 - 5) {}^(2) + ({0 - 4) {}^(2) } }`

`d = \sqrt{3 {}^(2) + {4}^(2) }`

`d = √(25)`

`d = 5`

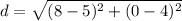
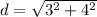
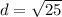
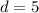
So our radius is 5.

So now we use the equation of center h,k.

`(x - h) {}^(2) + (y - k) {}^(2) = {r}^(2)`

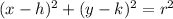
H is 4

K is 5

`(x - 4) {}^(2) + (y - 5) {}^(2) = 25`

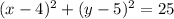
Above is sketch of graph.