Question

The equation for QR is 5y = -4x +41. Is QR tangent to Circle O at R? R (4,5) No, because the slope of OR times the slope of QR does not equal 1. No, because the slope of OR times the slope of QR does not equal -1. Yes, because the slope of OR times the slope of QR equals 1. Yes, because the slope of OR times the slope of QR equals -1,​

Answer 1

Check the picture below.

so the line OR has a slope of 5/4, what's the slope of QR anyway?

`5y=-4x+41\implies y=\cfrac{-4x+41}{5} \\\\\\ y=\stackrel{\stackrel{m}{\downarrow }}{\cfrac{-4}{5}} x+\cfrac{41}{5}\qquad \impliedby \qquad \begin{array}c \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

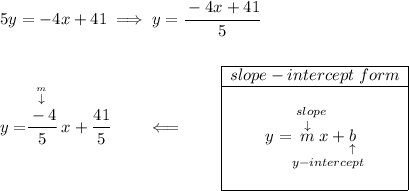
keeping in mind that perpendicular lines have negative reciprocal slopes, hmmm what's the slope of a line perpendicular to OR?

`\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{ \cfrac{5}{4}} ~\hfill \stackrel{reciprocal}{\cfrac{4}{5}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{4}{5} }}`

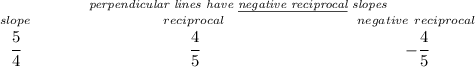
well, let's recall that the point of tangency in a circle is always at a right-angle, so if OR ⟂ QR then QR's slope should be -4/5, which it is, that means they're indeed perpendicular, and the product for two perpendicular slopes is -1, like in this case.