Question

What is the wavelength (in nm) of a 3 eV photon?

Answer 1

Answer:The wavelength of a photon with energy 3.0 eV is 413.57 nm and it is for visible light. This wavelength is of ultraviolet light.

Step-by-step explanation:

Answer 2

We are given –

• Energy of photon is = 3 eV

To find the wavelength of photon we have to use the Planck Expression.

`\qquad`
`\star\: \: \pink{\boxed{\frak{ E = hf}}}`

`\qquad`
`\bf \longrightarrow E = hf`

`\qquad`
`\sf \longrightarrow E = h * (c)/(\lambda) \: \: \purple{\bigg(\because f = (c)/(\lambda)\bigg)}`

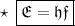
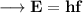
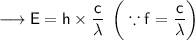
Where, E is the energy of photon and f is the frequency of photon & h's called Planck Constant.

`\qquad`
`\sf \longrightarrow h = 6.63* 10^(-34) \:Js`

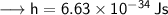
`\qquad` Speed of light, c =
`\sf 3*10^(8) \:m/s`

`\qquad\qquad\quad\underline{\sf{Substituting \ Values \ :}}`

⠀⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━━━

`\qquad`
`\bf \longrightarrow E = h * (c)/(\lambda)`

`\qquad`
`\bf \longrightarrow \lambda = (hc)/(E)`

`\qquad`
`\sf \longrightarrow \lambda = ( 6.63* 10^(-34)* 3* 10^(8))/( 3eV)`

`\qquad`
`\sf \longrightarrow \lambda = ( 6.63* 10^(-34)* 3* 10^(8))/( 3 * 1.6* 10^(-19))\: \:\purple{ \bigg(\because 1 eV= 1.6* 10^(-19) J\bigg)}`

`\qquad`
`\sf \longrightarrow \lambda = \frac{ 6.63 * \cancel{3}* 10^(-34+8)}{\cancel{3}* 1.6* 10^(-19)}`

`\qquad`
`\sf \longrightarrow \lambda = ( 6.63 * 10^(-26))/(1.6* 10^(-19))`

`\qquad`
`\sf \longrightarrow \lambda = 4.144 * 10^(-26+19)`

`\qquad`
`\sf \longrightarrow \lambda = 4.144 * 10^(-7)`

`\qquad`
`\sf \longrightarrow \lambda = 4.144* 10^(-7)\: m`

`\qquad`
`\sf \longrightarrow \lambda = 4.144 * 10^(-7)* 10^(9) \: nm\: \: \purple{\bigg(\because 1m = 10^9\: nm \bigg)}`

`\qquad`
`\sf \longrightarrow \lambda = 4.144 * 10^(-7+9)\: nm`

`\qquad`
`\sf \longrightarrow \lambda = 4.144 * 10^(2)\: nm`

`\qquad`
`\pink{\bf \longrightarrow \lambda = 414.4\: nm}`

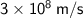
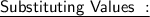
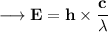
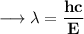
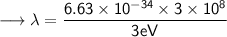
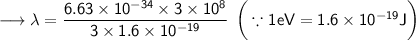
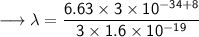
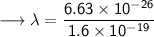
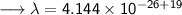
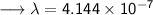
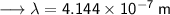
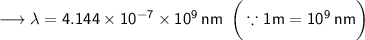
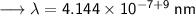
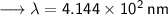
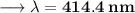
• Henceforth, wavelength will be 414.4nm.