Answer:
x = -4
Explanation:
Find the zeros of a function by setting the function equal to zero.
Basically, solve for x when p(x) = 0. Thus:
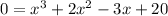
↓ seperate to factor out

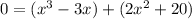
↓ factor out

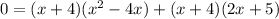
↓ simplify by combining the right part of each term
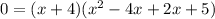
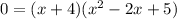
↓ split into two equations using the zero factor principle
(if
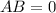 , then
, then
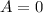 or
or
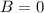 )
)
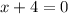
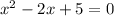
 ↓ complete the square
↓ complete the square
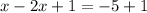
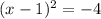

↑ no real solutions from this equation (sqrt. of negative)