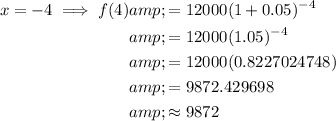Answer:
C. about 14,586; about 9,872
Explanation:
Given exponential function:
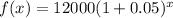
(where f(x) is the population of fish in a lake and x is the number of years).
To calculate the population in 4 years time, substitute x = 4 into the function:
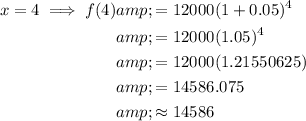
To calculate the population 4 years ago, substitute x = -4 into the function: