Question

if 4x ≤ g(x) ≤ 2x4 − 2x2 + 4 for all x, evaluate lim x→1 g(x). If 4x = g(x) = 2x4 – 2x2 + 4 for all x, evaluate lim g(x). x →1

Answer 1

Answer: 4

=============================================

Reason:

Let

• f(x) = 4x
• h(x) = 2x^4-2x^2+4

If we want to evaluate this limit

`\displaystyle \lim_{\text{x}\to1} g(\text{x})`

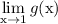
Then we need to evaluate these limits as well:
`\displaystyle \lim_{\text{x}\to1} f(\text{x}) \ \text{ and } \lim_{\text{x}\to1} h(\text{x})`

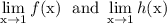
This is because g(x) is bound entirely by these lower and upper functions. Refer to the squeeze theorem for more information.

To evaluate those two other limits, we simply plug x = 1 into each function.

You should find that:

• f(1) = 4
• h(1) = 4

Each function results in 4 when x = 1. This then extends to the idea that f(x) approaches 4 when x approaches 1; similarly, h(x) approaches 4 when x approaches 1.

Therefore, g(x) must approach this same y value to be contained within both these boundaries. These two boundaries squeeze or pinch g(x) into one possible option here.