Answer:
(a) k = 0.04919 = 4.919% (4 s.f.)
(b) k = 0.007968 = 0.7958% (4 s.f.)
(c) The growth rate from 2016 to 2020 is significantly less.
(d) 2059, so during the 4 year period 2056 - 2060.
Explanation:
Given population in San Diego:
- 2012 = 1,309,000
- 2016 = 1,375,000
- 2020 = 1,386,000
Population Growth Formula
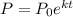
where:
- P = population at time t (in millions)
- P₀ = initial population
- e = Euler's number
- k = relative growth rate
- t = time elapsed
Part (a)
Let the population in 2012 be the "initial population":
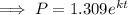
To find the growth rate (k) from 2012 to 2016, substitute t = 1 (since we want to find the growth rate over a period of 4 years) and P = 1.375 into the equation and solve for k:
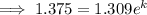
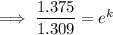
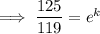
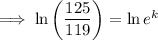
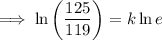
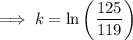
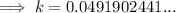
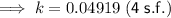
Therefore, the growth rate for the period of 4 years from 2012 to 2016 was 0.04919 = 4.919% (4 s.f.).
Part (b)
Let the population in 2016 be the "initial population":
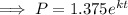
To find the growth rate (k) from 2016 to 2020, substitute t = 1 (since we want to find the growth rate over a period of 4 years) and P = 1.386 into the equation and solve for k:

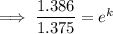
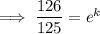
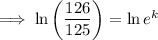
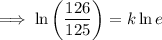
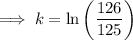
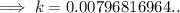
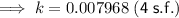
Therefore, the growth rate for the period of 4 years from 2016 to 2020 was 0.007968 = 0.7968% (4 s.f.).
Part (c)
The growth rate from 2012 to 2016 was 0.04919 = 4.919%
The growth rate from 2016 to 2020 was 0.007968 = 0.7968%
Therefore, as the growth rate from 2016 to 2020 is significantly less than the growth rate from 2012 to 2016, the growth of the population is slowing.
Part (d)
To calculate when the population of San Diego will reach 1.5 million if the current growth rate of 0.007968 continues, substitute P₀ = 1.386, k = 0.007968... and P = 1.5 into the equation and solve for t:
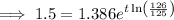
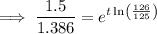

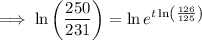
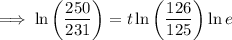
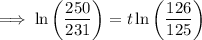
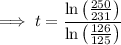
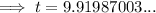
As each time period is 4 years long:
⇒ 2020 + 9.91987003... × 4 = 2059.67948
So the population of San Diego will reach 1.5 million during the year 2059, and so during the 4 year period 2056 - 2060.