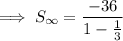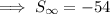Question

Given the pattern -36, 12, -4, ...

(a) Write an explicit formula for the pattern.

(b) Write a recursive formula for the pattern.

(c) Does the pattern converge or diverge? If it converges, to what value does it converge?

(d) If you added the terms in this pattern, would the sum converge or diverge? If it converges, to what value does it converge?

Answer 1

`\textsf{(a)} \quad a_n=-36\left((1)/(3)\right)^(n-1)`

`\textsf{(b)} \quad \begin{cases}a_1=-36\\\\a_n=(a_(n-1))/(3)\end{cases}`

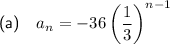
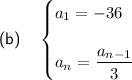
(c) Sequence converges to zero

(d) Sum converges to -54

Explanation:

Given sequence:

-36, -12, -4, ...

Since the common difference between terms is not constant, it is not an arithmetic sequence.

Divide each term by the previous term:

`\implies (-4)/(-12)=(1)/(3)`

`\implies (-12)/(-36)=(1)/(3)`

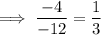
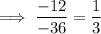
As the common ratio is the constant, this is a geometric sequence with common ratio (r) = ¹/₃.

Part (a)

An explicit formula allows you to find the nth term of the sequence.

`\boxed{\begin{minipage}{5.5 cm}\underline{Geometric sequence}\\\\$a_n=ar^(n-1)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\\phantom{ww}$\bullet$ $r$ is the common ratio.\\\phantom{ww}$\bullet$ $a_n$ is the $n$th term.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

Substitute a = -36 and r = ¹/₃ into the formula to write an explicit formula for the given sequence:

`\implies a_n=-36\left((1)/(3)\right)^(n-1)`

Part (b)

A recursive formula allows you to find the nth term of the sequence provided you know the value of the previous term in the sequence.

To obtain each term of the given sequence, divide the previous term by 3. Therefore, the recursive formula for the given sequence is:

`\begin{cases}a_1=-36\\\\a_n=(a_(n-1))/(3)\end{cases}`

Part (c)

`\lim_(n \rightarrow \infty)\;\;-36 \left((1)/(3) \right)^(n-1)=\lim_(n \rightarrow \infty)a_n=0`

`\textsf{As\; $n \rightarrow \infty$,\; $a_n \rightarrow 0$}`

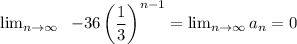
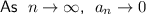
Therefore, the sequence converges, and the value it converges to is zero.

Part (d)

An infinite geometric series is said to be convergent if the absolute value of the common ratio is less than 1:

• |r| < 1

`\textsf (1)/(3) \right.`

`\boxed{\begin{minipage}{5.5 cm}\underline{Sum of an infinite geometric series}\\\\$S_(\infty)=(a)/(1-r)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\ \phantom{ww}$\bullet$ $r$ is the common ratio.\\\end{minipage}}`

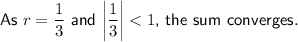
To find the value to which the sum of the infinite geometric series converges, substitute a = -36 and r = ¹/₃ into the formula:

`\implies S_(\infty)=(-36)/(1-(1)/(3))`

`\implies S_(\infty)=(-36)/((2)/(3))`

`\implies S_(\infty)=-54`