Answer: 9. 22.5 hours 10. 2 hours 55 minutes 11. 7.5 hours
Explanation:
9.
We take the capacity of the tank as one and the time of filling the tank
with pipe B as x
Hence, the speed of filling the tank with pipe A is 1/15 and the speed of filling the tank with pipe B is 1/x
Thus,
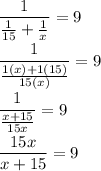
Multiply both parts of the equation by (x+15):
15x=9(x+15)
15x=9x+135
15x-9x=9x+135-9x
6x=135
Divide both parts of the equation by 6:
x=22.5 hours
10.
We take the capacity of the tank as one
Hence, the speed of filling the tank with pipe A is 1/7 and the speed of filling the tank with pipe B is 1/5
Thus,
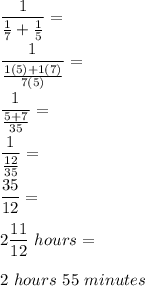
11.
We take the unmowed lawn as one and Joshua's lawn mowing time as x
Hence, Brianna's mowing speed is 1/5 and Joshua's mowing speed is 1/x
Thus,
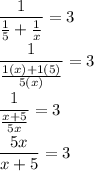
Multiply both parts of the equation by (x+5):
5x=3(x+5)
5x=3x+15
5x-3x=3x+15-3x
2x=15
Divide both parts of the equation by 2:
x=7.5 hours