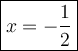Question

Find the axis of symmetry (AOS): x^2+x-6=0

Answer 1

To find the axis of symmetry (AOS) for the equation x^2+x-6=0, we can start by completing the square. This involves adding and subtracting the same value to the equation to make it have the form (x + a)^2 = b. In this case, we can add and subtract 9/4 to the equation to get:


`x^2 + x - 6 = (x + 1/2)^2 - 9/4`

This equation has the form
`(x + a)^2 = b`, where a = 1/2 and b = -9/4. The axis of symmetry (AOS) is the vertical line that passes through the point where the parabola defined by the equation opens. In this case, the AOS is the vertical line that passes through the point (-1/2, 0), which is the point where the parabola defined by the equation x^2 + x - 6 = 0 opens. Therefore, the AOS for this equation is the vertical line x = -1/2.

Answer 2

`x=-(1)/(2)`

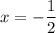
Explanation:

The axis of symmetry of a quadratic equation in the form y = ax² + bx + c, is a vertical line that passes through the vertex of the corresponding parabola, dividing it into two symmetrical halves.

The formula for the axis of symmetry is:

`\large\boxed{x=-(b)/(2a)}`

For the given equation, x² + x - 6 = 0:

• a = 1
• b = 1
• c = -2

Substitute the values of a and b into the formula:

`x=-(1)/(2(1))=-(1)/(2)`

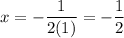
Therefore, the axis of symmetry of the given quadratic equation is:

`\large\boxed{x=-(1)/(2)}`