Answers:
a) 146.0781 ≤ (mean) ≤ 153.9219.
b) 144.8458 ≤ (mean) ≤ 155.1542.
Explanation:
1. 95% confidence interval.
1. Calculate σ(x-bar).
Check attached image 1.
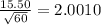
2. Calculate α/2.
"α" is the error that the confidence interval will have. Given a 95% confidence level, we know that the error is 5%; Error= 1 - Confidence.
α/2= 5%/2= 0.05/2= 0.025.
3. Find the absolute Z distribution value for α/2.
Since this sample's size is greater than 30, we use the normal distribution (Z). You can either use the probability tables or the Microsoft Excel tools to find the inverse of the Z distribution for this α/2 value (check attached image 2).
Z(α/2)= 1.96
4. Calculate the intervals.
Check attached image 3.
Lower limit: 150 - (1.96*2.0010)= 146.0781
Upper limit: 150 - (1.96*2.0010)= 153.9219
Interval:
146.0781 ≤ (x bar) ≤ 153.9219.
This interval means that there is a 95% chance that the repair cost of a refrigerator fall between $146.0781 and $153.9219, including.
---------------------------------------------------------------------------------------------------------
2. 99% confidence interval.
For this second interval, apply the same procedure as in the first interval, except this time we change the value of confidence, hence the value of the error changes aswell. These are the calculations and result:
1. Calculate σ(x-bar).
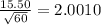
2. Calculate α/2.
Error= 1 - Confidence.
Error= 1- 0.99
Error= 0.01
α/2= 1%/2= 0.01/2= 0.005.
3. Find the absolute Z distribution value for α/2.
Z(α/2)= 2.58
4. Calculate the intervals.
Check attached image 3.
Lower limit: 150 - (2.58*2.0010)= 144.8458
Upper limit: 150 - (2.58*2.0010)= 155.1542
Interval:
144.8458 ≤ (x bar) ≤ 155.1542.
This interval means that there is a 99% chance that the repair cost of a refrigerator fall between $144.8458 and $155.1542, including.