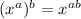Question

Another one? Please help.


Thank you so much!​

Answer 1

Hi there!

8.

Recall the following properties:

`(1)/(x^(-a)) = x^a\\\\x^0 = 1`

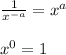
Thus, we can rearrange the expression in parts.

`(3x)^0 = 1\\\\x^4 = x^4\\\\y^(-4) = (1)/(y^4)\\\\(1)/(x^(-3)) = x^3\\\\(1)/(y^(-7)) = y^7`

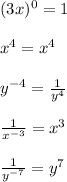
Now, combine these terms:

`(1) * x^4 * (1)/(y^4) * x^3 * y^7 = (x^4 * x^3 * y^7)/(y^4)`

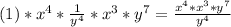
More properties:

`x^a * x^b = x^(a + b)\\\\(x^a)/(x^b) = x^(a - b)`

Rewrite:

`(1) = x^(4 + 3) * y^(7 - 4) = \boxed{\text{D) } x^7y^3}`

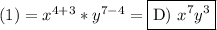
9)

Begin by solving the inside of the parenthesis.

`(3^2 + 3^0)^2 = (9 + 1)^2 = 10^2 = 100\\\\(6^(-2) + 3)^0 = 1\\\\100 - 1 = \boxed{ \text{ B. 99}}`

10)

Simplify the inside of the parenthesis using the above properties.

`((x^2y^5z^3)/(xy^7))^(-2) = ((xz^3)/(y^2))^(-2)`

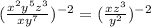
Since there is a negative in the outside exponent, we must take the reciprocal. (flip the numerator and denominator).

`=( (y^2)/(xz^3))^2`

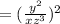
Square both the numerator and denominator.

Recall the property:

`(x^a)^b = x^(ab)`

`= (y^(2*2))/(x^2 * z^(3 * 2)) = \boxed{ \text{C. }(y^4)/(x^2z^6)}`