Question

Find the perimeter and total area of the compositor shape shown below. All measurements are given in inches.

Answer 1

`\bold{\huge{\pink{\underline{ Solution }}}}`

Given :-

• The radius of the hemisphere is 3 units
• The height of the hemisphere is 3 units
• The height of the triangle is 4 units
• The other two sides of triangle is 5 units each

To Find :-

• We have to find the area and perimeter of the composite solid ?

Let's Begin :-

We have given one composite which is composed of hemisphere and triangle

We know that,

Perimeter of hemisphere

`\bold{\red{ = }}{\bold{\red{\pi{r}}}}`

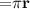
Perimeter of the triangle

`\bold{\pink{ = S + S + S }}`

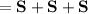
[ Both the figures have common base area ]

Therefore,

Total perimeter of the composite solid

`\sf{ = 5 + 5 + }{\sf{(22)/(7)}}{\sf{*{r}}}`

`\sf{ = 10 + }{\sf{(22)/(7)}}{\sf{*{3}}}`

`\sf{ = 10 + }{\sf{(66)/(7)}}`

`\sf{ = }{\sf{(70 + 66)/(7)}}`

`\sf{ = }{\sf{(136)/(7)}}`

`\bold{ = 19.42\: inches }`

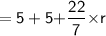
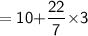
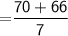
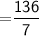
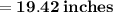
Thus, The perimeter of the composite solid is 19.42 inches

Now,

We have to find the area of composite solid

We know that,

Area of hemisphere

`\bold{\blue{ = }}{\bold{\blue{(1)/(2)}}}{\bold{\blue{\pi{r²}}}}`

`\sf{ = 0.5}{\sf{*{(22)/(7)}}}{\sf{*{ 3 }}}{\sf{*{ 3 }}}`

`\sf{ = 0.5}{\sf{*}}{\sf{(22)/(7)}}{\sf{*{ 9 }}}`

`\sf{ = 0.5}{\sf{*{(198)/(7)}}}`

`\sf{ = }{\sf{(99)/(7)}}`

`\bold{ = 14.14\: inches }`

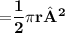
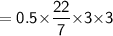
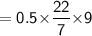
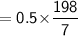
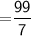
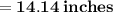
We also know that,

Area of triangle

`\bold{\purple{ = }}{\bold{\purple{(1)/(2)}}}{\bold{\purple{*{ Base}}}}{\bold{\purple{*{height }}}}`

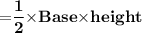
Subsitute the required values,

`\sf{ = }{\sf{(1)/(2)}}{\sf{*{ 4 }}}{\sf{*{3}}}`

`\sf{ = 2 }{\sf{*{ 3 }}}`

`\bold{ = 6\: inches }`

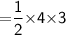
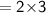
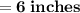
• [Note :- Both the figures have common base area. So for triangle base area will be 6/2 = 3 in.]

Therefore,

Total Area of the composite solid

`\sf{ = 14.14 + 6}`

`\bold{\red{ = 20.14\: inches }}`

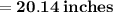
Hence, The perimeter and area of composite solid is 19.42 inches and 20.14 inches .