Answer:
Part 1:
-5, a multiplicity of 2
-1, a multiplicity of 1
4, a multiplicity of 3
7, a multiplicity of 1
Part 2:
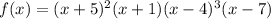
Explanation:
This question has to be done visually, and can is a little tricky, because depending on the way the graph intercepts the x-axis, there is going to be a different number of roots.
The roots are represented by the intersection of the function with the x-axis.
To start, take a look at the point
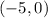 , which intercepts the x-axis like a parabola(quadratic function). This means that -5 is a "double root" of the function, or it represents two roots of the function.
, which intercepts the x-axis like a parabola(quadratic function). This means that -5 is a "double root" of the function, or it represents two roots of the function.
Now look at the point
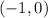 , which intercepts the x-axis in a linear way, meaning that -1 is simply a "single-root" of the function, or it only represents one root.
, which intercepts the x-axis in a linear way, meaning that -1 is simply a "single-root" of the function, or it only represents one root.
So for the next root, look at
 , which intercepts the x-axis like a cubic function. This means that 4 is is a "triple-root" of the function, and represents 3 roots of the function.
, which intercepts the x-axis like a cubic function. This means that 4 is is a "triple-root" of the function, and represents 3 roots of the function.
And finally, we have one final interception at
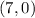 , and the interception is in a linear form, meaning 7 is simply a "single-root" to the function, or it only represents one root.
, and the interception is in a linear form, meaning 7 is simply a "single-root" to the function, or it only represents one root.
So we can conclude that the following are roots with their respective multiplicities
-5, a multiplicity of 2
-1, a multiplicity of 1
4, a multiplicity of 3
7, a multiplicity of 1
And totally, 2+1+3+1 gives us 7, which supports our answer because we know this is a seventh-degree polynomial.(1)
Now for Part 2
We simply take each root, and subtract it from x in our function, then apply our multiplicity as the exponent
So the function would be:
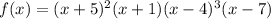 (2)
(2)
Hope this helps.