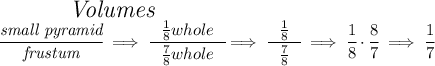Question

PLease help me ,really need help with explanation​

Answer 1

a)

Check the picture below.

b)

volume wise, we know the smaller pyramid is 1/8 th of the whole pyramid, so the volume of the whole pyramid must be 8/8 th.

Now, if we take off 1/8 th of the volume of whole pyramid, what the whole pyramid is left with is 7/8 th of its total volume, and that 7/8 th is the truncated part, because the 1/8 we chopped off from it, is the volume of the tiny pyramid atop.

Now, what's the ratio of the tiny pyramid to the truncated bottom?

`\stackrel{\textit{\Large Volumes}}{\cfrac{\textit{small pyramid}}{\textit{frustum}}\implies \cfrac{~~(1)/(8)whole ~~}{(7)/(8)whole}}\implies \cfrac{~~(1)/(8) ~~}{(7)/(8)}\implies \cfrac{1}{8}\cdot \cfrac{8}{7}\implies \cfrac{1}{7}`