Answer:
Explanation:
Part 1)
add their velocities
422+384= 806
now divide 6045 by 806 = 7.5 or 7 hours 30 minutes
7:30 = t hours:minutes
Part 2)
For this part we will need to employ Pythagoras theorem. we need the hypotenuse to be 1,997
so, when will plane traveling N , and plane traveling W be that far (1997)?
or
when does
 =
=
 +
+
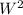
then we're also given that N = 422*t
and that W = 384 * t
so now our formula looks like
 =
=
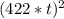 +
+
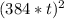
rewrite this so it's making clear math sense
 =
=
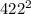 *
*
 +
+
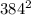 *
*

now pull out the

 = (
= (
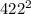 +
+
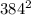 ) *
) *

now simplify some
3988009 = (178084 + 147456 ) *

now divide the left side by the numbers on the right
3988009 / (178084 + 147456 ) =

12.12044234 =

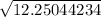 = t
= t
3.500063191 = t
so at 3 and a half hours, the planes will be 1997 miles apart
3:30 = t