Question

7. Sylvia went on a trip. The number of shirts she packed was 2 fewer than twice the number of pants

she packed. The total number of pairs of pants and shirts was 16.
A. Let x the number of pants she packed and let y = the number of shirts she packed. Write a system of
equations to represent the problem.
B. Solve the system of equations using substitution to find the number of shirts and pairs of pants Sylvia
brought.

Answer 1

`\textsf{A.} \quad \begin{cases}y=2x-2\\x+y=16\end{cases}`

`\textsf{B. \quad 6 pants and 10 shirts}`

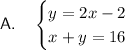
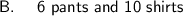
Explanation:

Part A

Given variables:

• Let x = the number of pants Sylvia packed.
• Let y = the number of shirts Sylvia packed.

If the number of shirts Sylvia packed was 2 fewer than twice the number of pants she packed:

`\implies y=2x-2`

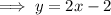
If the total number of pairs of pants and shirts was 16:

`\implies x+y=16`

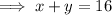
Therefore, the system of equations that represents the problem is:

`\begin{cases}y=2x-2\\x+y=16\end{cases}`

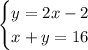
Part B

System of equations:

`\begin{cases}y=2x-2\\x+y=16\end{cases}`

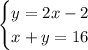
Substitute the first equation into the second equation and solve for x:

`\implies x+2x-2=16`

`\implies 3x-2=16`

`\implies 3x=18`

`\implies x=6`

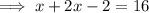
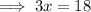
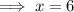
Substitute the found value of x into the first equation and solve for y:

`\implies y=2(6)-2`

`\implies y=12-2`

`\implies y=10`

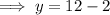
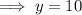
Therefore, Sylvia packed:

• 6 pants
• 10 shirts

Answer 2

10 shirts, 6 pants

Explanation:

Let y = the number of shirts

Let x = the number of pants

y + 2 = 2x

x + y = 16

y = 2x - 2

x + (2x - 2) = 16

3x = 18

x = 6

y + 6 = 16

y = 10