Question

Write the rate law for the following reaction given that the order of A = 2, B = 1, and C = 0. A + B + C ———> D + E

If the concentration of C is doubled, what will happen to the rate of the reaction?

Answer 1

The rate law is:

`\displaystyle \text{Rate} & = k[A]^2[B]`

Doubling the concentration of C will have no effect on the rate of the reaction.

Step-by-step explanation:

We want to write the rate law for the reaction:

`\displaystyle A + B + C \longrightarrow D + E`

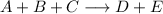
Where the order of A, B, and C are 2, 1, and 0, respectively.

The rate law will have the form:

`\displaystyle \text{Rate} = k [A]^m[B]^n[C]^p`

Where m, n, and p are their respective order of reactions.

Hence, the rate law is:

`\displaystyle \begin{aligned} \text{Rate} & = k[A]^2[B][C]^0\\ \\ & = k[A]^2[B] \end{aligned}`

Because the order of reaction to C is 0, changing its concentration will have no effect on the rate law.