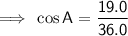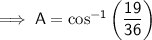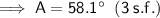Question

A piece of conduit 39.0 ft long cuts across the corner of a room, as shown in the illustration. Find length x and Angle A. Round each answer to the appropriate number of significant digits

Answer 1

x = 30.6 ft

A = 58.1°

Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{Pythagoras Theorem} \\\\$a^2+b^2=c^2$\\\\where:\\ \phantom{ww}$\bullet$ $a$ and $b$ are the legs of the right triangle. \\ \phantom{ww}$\bullet$ $c$ is the hypotenuse (longest side) of the right triangle.\\\end{minipage}}`

As the triangle is a right triangle, use Pythagoras Theorem to find length x.

`\implies x^2+19^2=36^2`

`\implies x^2+361=1296`

`\implies x^2=935`

`\implies x=√(935)`

`\implies x=30.6\; \sf ft \;\; (3\;s.f.)`

`\boxed{\begin{minipage}{9 cm}\underline{Cos trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

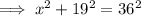
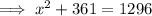
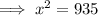
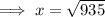
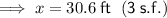
From inspection of the given right triangle:

• θ = A
• A = 19.0 ft
• H = 36.0 ft

Substitute the values into the formula and solve for A:

`\implies \sf \cos A=(19.0)/(36.0)`

`\implies \sf A= \cos^(-1)\left((19)/(36)\right)`

`\implies \sf A=58.1^(\circ)\;\;(3\;s.f.)`