Question

An Atwood's machine consists of blocks of masses

m1 = 11.0 kg
and
m2 = 19.0 kg
attached by a cord running over a pulley as in the figure below. The pulley is a solid cylinder with mass
M = 7.90 kg
and radius
r = 0.200 m.
The block of mass m2 is allowed to drop, and the cord turns the pulley without slipping.

Answer 1

Step-by-step explanation:

Given that:

`mass \ m_ 1 = 11.0 \ kg`

`mass \ m_2 = 19.0 \ kg`

`mass \ of \ the \ pulley\ M = 7.90 \ kg`

`Radius \ of \ the \ pulley = 0.200\ m`

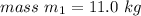
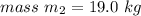
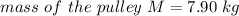
1) Provided that the mass in
`m_2` is greater than the mass we have in
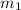`m_1`, then likewise the tension we have in
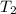`T_2` will be greater than the tension in
`T_1`

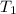
Using Newton's second law to mass
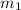`m_1`, we have:

`m_2g - T_2 = m_2 a \\ \\ T_1 = m_1 g +m_1 a \\ \\ T_1= m_1 (g+a) --- (1)`

By using the second law, we have:

`m_2g - T_2 = m_2a \\ \\ T_2 = m_2 (g-a)---(2)`

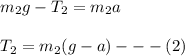
For the pulley, let's use the torque equation, so we have:

`T_2 r -T_1 r = I \alpha \\ \\ T_2r -T_1r = \Big ( (Mr^2)/(2)\Big) (a)/(r) \\ \\ T_2 -T_1 = (Ma)/(2) ---- (3)`

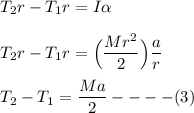
Altogether, from equation (1)(2) and (3), we have:

`m_2(g-a) -m_1 (g+a) = (Ma)/(2) \\ \\ m_2g -m_2a -m_1g-m_1a = (Ma)/(2) \\ \\ a = ((m_2 -m_1) g)/((m_1 + m_2 + (M)/(2))) \\ \\ a = ((19.0 \ kg - 11.0 \ kg ) ( 9.8 \ m/s^2))/((19.0 \ kg + 11.0 \ kg + (7.90 \ kg )/(2) ))`

`a = 2.31 \ m/s^2`

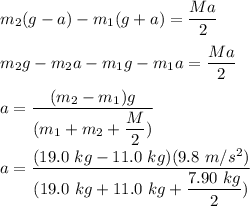
Also; from equation (1), the tension in the string is:

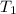`T_1` = (11.0 kg ) ( 9.8 + 2.31) m/s²

`T_1` = 133.21 N

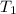`T_1` ≅ 133 N

From equation (2):

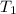`T_1` = m_2(g-a)

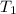`T_1` = (19.0 kg) ( 9.8 - 2.31) m/s²

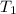`T_1` = 142.31 N

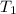`T_1` = 142 N