Answer:
y > -2/3x + 2, y
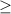 x
x
Explanation:
Knowledge Needed
A system of linear inequalities is graphing 2 lines.
If the line's y side is less than it's x-side (y </
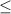 x), shade below.
x), shade below.
If the line's y side is greater than it's x-side (y </
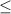 x), shade above.
x), shade above.
If the line is dotted, it is < or >.
If the line is filled in, it is
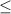 or
or
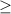 .
.
Where both regions are shaded is the solution.
Question
Examine the dotted line.
1) We know it is < or > because it is dotted.
2) We know it is y > .... because if it was less than, it would be shaded below, which is impossible because the shaded region is above.
3) We know the y-intercept, when x=0, is 2.
4) We know the slope, how much the y-value of a line changed when the x-value changes by 1, is -2/3.
y > -2/3x + 2
Examine the solid line.
1) We know it is
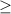 or
or
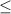 because it is solid.
because it is solid.
2) We know it is y
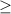 .... because if it was less than, it would be shaded below, which is impossible because the shaded region is above.
.... because if it was less than, it would be shaded below, which is impossible because the shaded region is above.
3) We know the y-intercept, when x=0, is 0.
4) We know the slope, how much the y-value of a line changed when the x-value changes by 1, is 1.
y
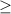 1x + 0
1x + 0
y
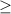 x
x
The solution to the linear inequality is when both lines are shaded in (true), which means both lines are the solution together.
y > -2/3x + 2, y
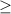 x
x