Question

Rank the following objects by their accelerations down an incline (assume each object rolls without slipping) from least to greatest:

a. Hollow Cylinder
b. Solid Cylinder
c. Hollow Sphere
d. Solid Sphere

Answer 1

The objects are ranked by their accelerations down an incline, from least to greatest, as follows: hollow cylinder, hollow sphere, solid cylinder, and solid sphere, with the solid sphere accelerating the fastest due to having the least moment of inertia.

Step-by-step explanation:

To rank the objects by their accelerations down an incline from least to greatest, we need to consider the moment of inertia of each object, which determines how much of the gravitational potential energy is converted into rotational kinetic energy vs. translational kinetic energy when rolling down an incline. Objects with a larger moment of inertia will have a greater proportion of their energy as rotational energy, and thus will accelerate down the incline more slowly. Here is the correct order based on their moment of inertia, from least to greatest acceleration:

1. Hollow cylinder (greatest moment of inertia, slowest acceleration)
2. Hollow sphere
3. Solid cylinder
4. Solid sphere (least moment of inertia, greatest acceleration)

The moment of inertia for a solid sphere is less than that of a solid cylinder, which in turn is less than that for a hollow sphere, and the hollow cylinder has the greatest moment of inertia of all. Thus, the solid sphere rolls down the fastest, and the hollow cylinder the slowest.

Answer 2

acceleration are

hollow cylinder < hollow sphere < solid cylinder < solid sphere

Step-by-step explanation:

To answer this question, let's analyze the problem. Let's use conservation of energy

Starting point. Highest point

Em₀ = U = m g h

Final point. To get off the ramp

Em_f = K = ½ mv² + ½ I w²

notice that we include the kinetic energy of translation and rotation

energy is conserved

Em₀ = Em_f

mgh = ½ m v² +1/2 I w²

angular and linear velocity are related

v = w r

w = v / r

we substitute

mg h = ½ v² (m + I / r²)

v² = 2 gh
`(m)/(m+ (I)/(r^2) )`

v² = 2gh
`(1)/(1 + (I)/(m r^2) )`

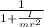
this is the velocity at the bottom of the plane ,, indicate that it stops from rest, so we can use the kinematics relationship to find the acceleration in the axis ax (parallel to the plane)

v² = v₀² + 2 a L

where L is the length of the plane

v² = 2 a L

a = v² / 2L

we substitute

a =
`g \ (h)/(L) \ (1)/(1+ (I)/(m r^2 ) )`

let's use trigonometry

sin θ = h / L

we substitute

a = g sin θ \ \frac{h}{L} \ \frac{1}{1+ \frac{I}{m r^2 } }

the moment of inertia of each object is tabulated, let's find the acceleration of each object

a) Hollow cylinder

I = m r²

we look for the acerleracion

a₁ = g sin θ
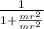`(1)/(1 + (mr^2 )/(m r^2 ) )`1/1 + mr² / mr² =

a₁ = g sin θ ½

b) solid cylinder

I = ½ m r²

a₂ = g sin θ
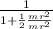`(1)/(1 + (1)/(2) (mr^2)/(mr^2) )` = g sin θ
`(1)/(1+ (1)/(2) )`

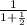
a₂ = g sin θ ⅔

c) hollow sphere

I = 2/3 m r²

a₃ = g sin θ
`(1)/(1 + (2)/(3) )`

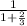
a₃ = g sin θ
`(3)/(5)`

d) solid sphere

I = 2/5 m r²

a₄ = g sin θ
`(1 )/(1 + (2)/(5) )`

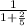
a₄ = g sin θ
`(5)/(7)`

We already have all the accelerations, to facilitate the comparison let's place the fractions with the same denominator (the greatest common denominator is 210)

a) a₁ = g sin θ ½ = g sin θ
`(105)/(210)`

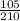
b) a₂ = g sinθ ⅔ = g sin θ
`(140)/(210)`

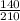
c) a₃ = g sin θ
`(3)/(5)`= g sin θ
`(126)/(210)`

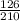
d) a₄ = g sin θ
`(5)/(7)` = g sin θ
`(150)/(210)`

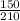
the order of acceleration from lower to higher is

a₁ <a₃ <a₂ <a₄

acceleration are

hollow cylinder < hollow sphere < solid cylinder < solid sphere