Answer:
acceleration are
hollow cylinder < hollow sphere < solid cylinder < solid sphere
Step-by-step explanation:
To answer this question, let's analyze the problem. Let's use conservation of energy
Starting point. Highest point
Em₀ = U = m g h
Final point. To get off the ramp
Em_f = K = ½ mv² + ½ I w²
notice that we include the kinetic energy of translation and rotation
energy is conserved
Em₀ = Em_f
mgh = ½ m v² +1/2 I w²
angular and linear velocity are related
v = w r
w = v / r
we substitute
mg h = ½ v² (m + I / r²)
v² = 2 gh
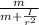
v² = 2gh
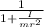
this is the velocity at the bottom of the plane ,, indicate that it stops from rest, so we can use the kinematics relationship to find the acceleration in the axis ax (parallel to the plane)
v² = v₀² + 2 a L
where L is the length of the plane
v² = 2 a L
a = v² / 2L
we substitute
a =
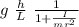
let's use trigonometry
sin θ = h / L
we substitute
a = g sin θ \ \frac{h}{L} \ \frac{1}{1+ \frac{I}{m r^2 } }
the moment of inertia of each object is tabulated, let's find the acceleration of each object
a) Hollow cylinder
I = m r²
we look for the acerleracion
a₁ = g sin θ
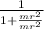 1/1 + mr² / mr² =
1/1 + mr² / mr² =
a₁ = g sin θ ½
b) solid cylinder
I = ½ m r²
a₂ = g sin θ
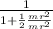 = g sin θ
= g sin θ
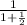
a₂ = g sin θ ⅔
c) hollow sphere
I = 2/3 m r²
a₃ = g sin θ
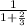
a₃ = g sin θ

d) solid sphere
I = 2/5 m r²
a₄ = g sin θ
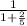
a₄ = g sin θ

We already have all the accelerations, to facilitate the comparison let's place the fractions with the same denominator (the greatest common denominator is 210)
a) a₁ = g sin θ ½ = g sin θ
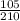
b) a₂ = g sinθ ⅔ = g sin θ
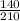
c) a₃ = g sin θ
 = g sin θ
= g sin θ
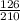
d) a₄ = g sin θ
 = g sin θ
= g sin θ
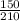
the order of acceleration from lower to higher is
a₁ <a₃ <a₂ <a₄
acceleration are
hollow cylinder < hollow sphere < solid cylinder < solid sphere