Answer:
(a) The table

(b) See attachment for graph
(c) He swapped the values of the x and y coordinates for one another
Explanation:
Given
See attachment for complete question
Solving (a): Complete the table
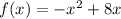
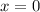 :
:
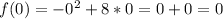
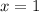 :
:
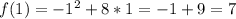
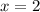 :
:
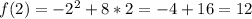
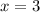 :
:
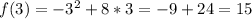
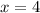 :
:
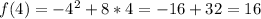
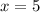 :
:
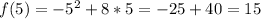
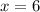 :
:
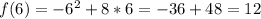
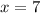 :
:
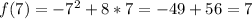
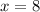 :
:
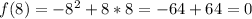
So, the complete table is:

Solving (b): Plot the graph
See attachment 2 for graph
Solving (c): Why he was marked as incorrect
By comparing the new attached graph (in b) and the graph of the original question, one will notice that the values of the x and y coordinates are switched.
This is why he was marked as incorrect.