Answer:
a) ( 31.92 < μ < 33.88 )
The confidence interval is not very different from the confidence interval given in the question
b) ( 31.74 , 34.66 )
Explanation:
n = 250
x ( mean ) = 32.9
std = 6.9
95% confidence interval
df = n - 1 = 250 - 1 = 249
a) construct confidence interval estimate
calculate for the margin of error
=
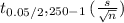 ( using excel function: T.INV.2T(0.025,249) )
( using excel function: T.INV.2T(0.025,249) )
= 2.255 ( 6.9 / 15.81 )
= 0.98
Hence the confidence interval for the population
= ( x - 0.98 < μ < x + 0.98 )
= ( 31.92 < μ < 33.88 )
The confidence interval is not very different from the confidence interval given in the question
b) when n = 19
x = 33.2 and std = 2.6
margin of error =
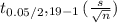 = 2.45 * ( 2.6 / 4.36 ) = 1.46
= 2.45 * ( 2.6 / 4.36 ) = 1.46
confidence interval
= ( 33.2 - 1.46 , 33.2 + 1.46 )
= ( 31.74 , 34.66 )