Question

Which of the points below does not lie on the curve y = x² ?

A: (3/2, 9/2) B: (-1,1) C: (4,16) D: (1/2,1/4)​

Answer 1

Point A does not lie on the curve y = x²

Explanation:

Given points:

`\sf A: \left((3)/(2), (9)/(2)\right)`

`\sf B: \left(-1,1 \right)`

`\sf C: \left(4,16 \right)`

`\sf D: \left((1)/(2), (1)/(4)\right)`

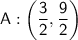
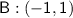
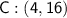
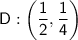
To determine if the given points lie on the curve y = x², simply substitute the x-value of each point into the equation and compare y-values.

Point A

`\boxed{\begin{aligned}x=(3)/(2) \implies y&=\left((3)/(2) \right)^2\\\\y&=(3^2)/(2^2)\\\\y&=(9)/(4)\end{aligned}}`

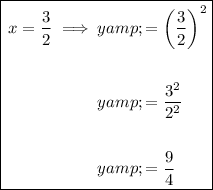
As 9/4 ≠ 9/2, point A does not lie on the curve.

Point B

`\boxed{\begin{aligned}x= -1\implies y&=\left(-1 \right)^2\\y&=1\end{aligned}}`

As 1 = 1, point B does lie on the curve.

Point C

`\boxed{\begin{aligned}x=4 \implies y&=\left( 4\right)^2\\y&=16\end{aligned}}`

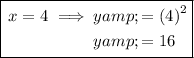
As 16 = 16, point C does lie on the curve.

Point D

`\boxed{\begin{aligned}x=(1)/(2) \implies y&=\left((1)/(2) \right)^2\\\\y&=(1^2)/(2^2)\\\\y&=(1)/(4)\end{aligned}}`

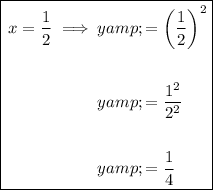
As 1/4 = 1/4, point D does lie on the curve.