Answer:
Increasing on the interval: (-2, 0) ∪ (2, ∞)
Decreasing on the interval: (-∞, -2) ∪ (0, 2)
Explanation:
A function is increasing when f'(x) > 0
A function is decreasing when f'(x) < 0
Therefore, to find the intervals for which the function is increasing and decreasing, differentiate the given function.

Given function:
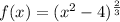
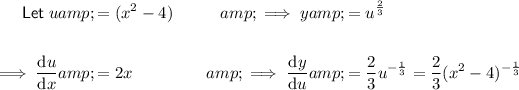
Therefore:
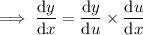
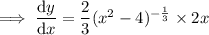
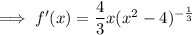
![\implies f'(x)=\frac{4x}{3 \sqrt[3]{x^2-4}}}](https://img.qammunity.org/2023/formulas/mathematics/college/quiwiow3vdbrcoxash7mvcj4eeph71d3oq.png)
Stationary points occur when f'(x) = 0:
![\implies \frac{4x}{3 \sqrt[3]{x^2-4}}}=0](https://img.qammunity.org/2023/formulas/mathematics/college/x4e2fyf4elcu7yqa5rtsxyb4k3xgj1ki8q.png)
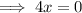
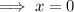
Therefore, the function has is a stationary point (turning point) when x = 0.
The derivative is undefined when the denominator equals zero.
The denominator equals zero when x² = 4, so when x = ±2.
The derivative is positive when x > 2 and negative when x < -2.
Therefore, determine the nature of the derivative in the intervals between the stationary point x = 0 and x = ±2.
![\implies f'(-1)=\frac{4(-1)}{3 \sqrt[3]{(-1)^2-4}}}=(\rm negative)/(\rm negative)= \rm positive > 0](https://img.qammunity.org/2023/formulas/mathematics/college/tsh3ptkksyh0vuz6wof865wgylong9z0y5.png)
![\implies f'(1)=\frac{4(1)}{3 \sqrt[3]{(1)^2-4}}}=(\rm positive)/(\rm negative)= \rm negative < 0](https://img.qammunity.org/2023/formulas/mathematics/college/t1c0baglj5603d22iieqy20fzhmikoup0c.png)
Therefore, the function is:
- Increasing on the interval: (-2, 0) ∪ (2, ∞)
- Decreasing on the interval: (-∞, -2) ∪ (0, 2)