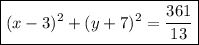Answer:
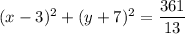
Explanation:
The tangent of a circle is always perpendicular to the radius.
Therefore, the center is on a line that is perpendicular to the tangent.
Rearrange the equation of the tangent to make y the subject:
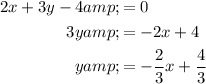
Therefore, the slope of the tangent line is -²/₃.
If two lines are perpendicular to each other, their slopes are negative reciprocals. Therefore, the slope of the perpendicular line is ³/₂.
To write the equation of the line perpendicular to the tangent, substitute the found slope and the center point into the point-slope formula:

The point on the circle is the point of intersection of the tangent line and the perpendicular line.
To find the point of intersection, substitute the equation for the perpendicular line into the equation for the tangent line:
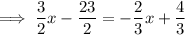
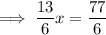
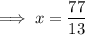
Substitute the found value of x into one of the linear equations and solve for y:
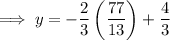

Therefore, the point of intersection and hence the point on the circle is:


To find r², substitute the given center of the circle (3, -7) and the found point into the equation of the circle:
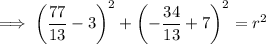
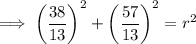
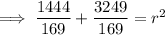
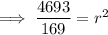
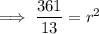
Therefore, the equation of the circle whose center is P(3, -7) and tangent to 2x+3y-4=0 is: