Question

- Celeste had 3¢ on Day 1. She had three times that

much on Day 2. On Day 3 she had three times as
much as she had on Day 2. If she continues this
pattern, on what day will she have 2,187¢?

Answer 1

Day 7

Explanation:

Given information:

• Celeste had 3¢ on Day 1.
• She had three times that much on Day 2.
• On Day 3 she had three times as much as she had on Day 2.

Therefore, each day Celeste has three times as much as she had the previous day.

This can be expressed by the recursive rule:

`\begin{cases}a_n=3a_(n-1)\\a_1=3\end{cases}`

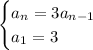
Therefore:

`\textsf{Day 2}: \quad a_2=3 \cdot a_(1)=3 \cdot 3=9`

`\textsf{Day 3}: \quad a_3=3 \cdot a_(2)=3 \cdot9=27`

`\textsf{Day 4}: \quad a_4=3 \cdot a_(3)=3 \cdot 27=81`

`\textsf{Day 5}: \quad a_5=3 \cdot a_(4)=3 \cdot 81=243`

`\textsf{Day 6}: \quad a_6=3 \cdot a_(5)=3 \cdot 243=729`

`\textsf{Day 7}: \quad a_7=3 \cdot a_(6)=3 \cdot 729=2187`

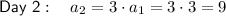
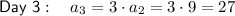
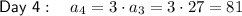
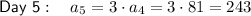
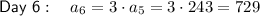
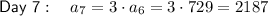
So the day on which Celeste will have 2,187¢ is day 7.