Question

The average weight of a package of rolled oats is supposed to be at most 18 ounces. A sample of 18 packages shows a mean of 18.20 ounces with a sample standard deviation of 0.50 ounces. (a) at the 5 percent level of significance, is the true mean larger than the specification

Answer 1

Pvalue of 0.0446 < 0.05, which means that we reject the null hypothesis and accept the alternative hypothesis, that the true mean is larger than the specification.

Explanation:

The average weight of a package of rolled oats is supposed to be at most 18 ounces.

This means that the null hypothesis is:

`H_(0): \mu \leq 18`

Is the true mean larger than the specification?

Due to the question asked, the alternate hypothesis is:

`H_(a): \mu > 18`

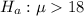
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

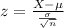
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
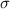`\sigma` is the standard deviation and n is the size of the sample.

18 is tested at the null hypothesis:

This means that
`\mu = 18`

A sample of 18 packages shows a mean of 18.20 ounces with a sample standard deviation of 0.50 ounces.

This means that
`n = 18, X = 18.2, \sigma = 0.5`

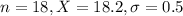
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (18.2 - 18)/((0.5)/(√(18)))`

`z = 1.7`

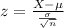
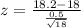
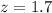
Pvalue of the test:

Probability of finding a sample mean above 18.2, which is 1 subtracted by the pvalue of z = 1.7.

Looking at the z-table, z = 1.7 has a pvalue of 0.9554.

1 - 0.9554 = 0.0446

0.0446 < 0.05, which means that we reject the null hypothesis and accept the alternative hypothesis, that the true mean is larger than the specification.