Question

PLEASE HELP WILL GIVE 100 POINTS

Answer 1

• 72y or -72y

-----------------------------

We are given a binomial and need to add a monomial to make it a perfect square.

Recall the identities for a square of a sum or difference of two numbers:

• (a ± b)² = a² ± 2ab + b²

Analyze the given and compare with the identity above:

• 16y² + ... + 81

• Here 16y² = (4y)² and 81 = 9², so a = 4y and b = 9.

To complete the square we need to add ± 2ab, which is:

• ± 2ab = ± 2(4y*9) = ± 72y

By adding this we get:

• 16y² + 72y + 81 = (4y + 9)²

or

• 16y² + (-72y) + 81 = (4y - 9)²

Answer 2

72y

Explanation:

Perfect square monomials are in the form:

`x^2+bx+\left((b)/(2)\right)^2`

They factor as:

`\left(x + (b)/(2)\right)^2`

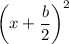
To find the middle term of this polynomial, first factor 16 out of the expression.

`16(y^2 \: + \: ?+5.0625)`

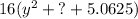
We know that the middle term will be in the form
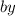`by`, and the last term will be in the form
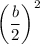`\left((b)/(2)\right)^2`. Using this information, we can solve for b.

`5.0625 = \left((b)/(2)\right)^2`

`√(5.0625) = (b)/(2)\right`

`4.5 = b`

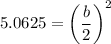
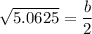
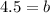
Then, we can substitute that into the term
`by`.

`16(y^2 + 4.5y+5.0625)`

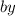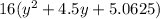
Finally, distribute the 16 and then take the middle term as the answer.

`16y^2 + 72y+81`

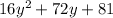
72y