Divide by 12 to go from the APR to the monthly interest rate
(9.5%)/12 = 0.7916667%
The decimal form is 0.007916667 approximately.
Multiply this with the starting balance $1367.90 and we get:
0.007916667*1367.90 = 10.8292 which rounds to 10.83
The interest payment for the 1st month is $10.83; which means the principal payment would be 400-10.83 = 389.17
This principal payment will then drop the balance from $1367.90 to 1367.90-389.17 = 978.73 dollars.
The value $978.73 is now the starting balance of the 2nd month. This process of...
- (a) Compute the interest
- (b) Subtract the interest from the $400 monthly payment to get the principal (with the exception of the last month as shown below)
- (c) Subtract the principal from the starting balance to get the ending balance.
is repeated until the balance is $0.
This is what the table would look like

Many credit card companies and banks offer free calculators on their website, or you can find similar free calculators online elsewhere, that will quickly calculate a table like shown above. It is called an amortization table or amortization schedule.
With the exception of the 4th month, each row has the principal and interest add to the $400 monthly payment. The last row will have a payment of 1.51+191.12 = 192.63 dollars.
The total amount paid back would be 400+400+400+192.63 = 1392.63 dollars. This is the sum of the values in the "payment" column.
-------------------------------------------------------------------------
Here's another way to determine the answer.
The monthly payment formula is
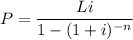
where,
- P = monthly payment
- L = loan amount, aka starting balance
- i = monthly interest rate in decimal form
- n = number of months
In this case,
- P = 400
- L = 1367.90
- i = 0.007916667 approximately (calculated earlier)
- n = unknown
Let's solve for the variable n. We'll need logarithms to isolate the exponent.
Part 1
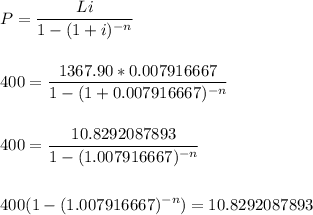
Part 2

Part 3

Each decimal value is approximate.
That value of n then rounds up to the nearest integer n = 4
We do not round to n = 3 since that would be one month short, as shown in the table above.
You can use a graphing calculator to quickly solve that equation for the variable n. It can be used as a way to visually confirm the answer.