Question

You invest $1000 in an account that has an annual interest rate of 4%, compounded monthly for 12 years. What is the equivalent interest rate and how many times will the money be compounded?

3% and 144 times
3% and 4 times
O 0.33% and 1 time
0.33% and 144 times

Answer 1

The equivalent interest rate is 56.916% and the money will be compounded 144 times.

Step-by-step explanation:

To calculate the equivalent interest rate and the number of times the money will be compounded, we can use the formula for compound interest:
`A = P(1 + r/n)^(^n^t^)`

where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times the interest is compounded per year, and t is the number of years.

In this case, P = $1000, r = 4% = 0.04, n = 12 (compounded monthly), and t = 12 years. Plugging these values into the formula, we have:

`A = 1000(1 + 0.04/12)^(^1^2^*^1^2^)`

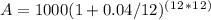
A ≈ $1569.16

Therefore, the final amount after 12 years is approximately $1569.16. The equivalent interest rate is the difference between the final amount and the principal amount, divided by the principal amount:

Equivalent Interest Rate = (A - P)/P = (1569.16 - 1000)/1000 = 0.56916 or 56.916%

The money will be compounded 12 * 12 = 144 times over the 12-year period.