Answer:
x = 13.6 (1 dp)
Explanation:
Using the following trig ratio to calculate the base of each triangle:
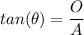
where
 is the angle, O is the side opposite the angle and A is the side adjacent to the angle.
is the angle, O is the side opposite the angle and A is the side adjacent to the angle.
Left triangle
Given:
 = 39
= 39- O = 6
- A =
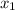

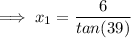
Right triangle
Given:
 = 44
= 44- O = 6
- A =
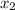
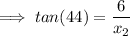
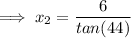
Length of x

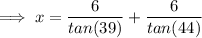
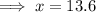 (1 dp)
(1 dp)