Question

(1 point) A bucket that weighs 3.6 pounds and a rope of negligible weight are used to draw water from a well that is 78 feet deep. The bucket is filled with 38 pounds of water and is pulled up at a rate of 2.9 feet per second, but water leaks out of a hole in the bucket at a rate of 0.1 pounds per second. Find the work done pulling the bucket to the top of the well. Your answer must include the correct units. (You may enter lbf or lb*ft for ft-lb.)

Answer 1

The total work done in pulling the bucket to the top of the well is approximately 3,139.1 ft·lb

Explanation:

The given parameters are;

The mass of the bucket, W = 3.6 pounds

The depth of the well, h = 78 feet deep

The mass of water in the bucket = 38 ponds

The rate at which the water is pulled up = 2.9 feet per second

The rate at which water is leaking from the bucket,
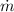`\dot m` = 0.1 pounds per second

We separate and find the work done for lifting the bucket and the water individually, then we add the answers to get the solution to the question as follows;

The work done in lifting bucket empty from the well bottom,
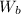`W_b` = W × h

∴
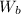`W_b` = 3.6 pounds × 78 feet = 280.8 ft-lb

The work done in lifting bucket empty from the well bottom,
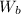`W_b` = 280.8 ft-lb

The time it takes to lift the bucket from the well bottom to the top, 't', is given as follows;

Time, t = Distance/Velocity

The time it takes to pull the bucket from the well bottom is therefore;

t = 78 ft./(2.9 ft./s) ≈ 26.897

The time it takes to pull the bucket from the well bottom to the top, t ≈ 26.897 s

The mass of water that leaks out from the bucket before it gets to the top, m₂, is therefore;

m₂ =
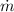`\dot m` × t

∴ m₂ = 0.1 lbs/s × 26.897 s = 2.6897

The mass of the water that leaks, m₂ = 2.6897 lbs

The mass of water that gets to the surface m₃ = m - m₂

∴ m₃ = 38 lbs - 2.6897 lbs ≈ 35.3103 lbs

Given that the water leaks at a constant rate the equation representing the mass of the water as it is lifted can b represented by a straight line with slope, 'm' given as follows;

The slope of the linear equation m = (38 lbs - 35.3103 lbs)/(78 ft. - 0 ft.) = 0.03448
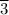`\overline 3` lbs/ft.

Therefore, the equation for the weight of the water 'w' can be expressed as follows;

w = 0.03448
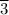`\overline 3`·y + c

At the top of the well, y = 0 and w = 38

∴ 35.3103 = 0..03448
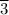`\overline 3` × 0 + c

c = 35.3103

∴ w = 0.03448
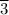`\overline 3`·y + 35.3103

The work done in lifting the water through a small distance, dy is given as follows;

(0.03448
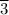`\overline 3`·y + 38) × dy

The work done in lifting the water from the bottom to the top of the well,
`W_(water)`, is given as follows;

`W_(water) = \int\limits^(78)_0 {0.03448\overline 3 \cdot y + 35.3103 } \, dy`

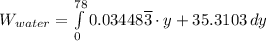
`\therefore W_(water) = \left [ {(0.03448\overline 3 \cdot y^2)/(2) + 35.3103 \cdot y\right ]^(78)_0`

`W_(water)` = (0.034483/2 × 78^2 + 35.3103 × 78) - (0.034483 × 0 + 38 × 0) ≈ 2,859.1

The work done in lifting only the water,
`W_(water)` ≈ 2,859.1 ft-lb

The total work done, in pulling the bucket to the top of the well, W =
`W_b` +
`W_(water)`

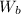∴ W = 2,859.1 ft.·lb + 280.8 ft.·lb ≈ 3,139.1 ft·lb

The total work done, in pulling the bucket to the top of the well, W ≈ 3,139.1 ft·lb.