Answer: If in a prior study, a sample of 200 people showed that 40 traveled overseas last year, then n= 385
If no estimate of the sample proportion is available , then n= 601
Explanation:
Let p be the prior population proportion of people who traveled overseas last year.
If p is known, then required sample size =
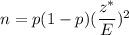
z-value for 95% confidence = 1.96
E = 0.04 (given)
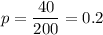
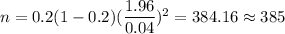
Required sample size = 385
If p is unknown, then required sample size =
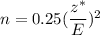
, where E = Margin of error , z* =critical z-value.
z-value for 95% confidence = 1.96
E = 0.04 (given)
So,
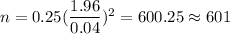
Required sample size = 601.