Question

A researcher wishes to be 95% confident that her estimate of the true proportion of individuals who travel overseas is within 4% of the true proportion. Find the sample necessary if, in a prior study, a sample of 200 people showed that 40 traveled overseas last year. If no estimate of the sample proportion is available, how large should the sample be

Answer 1

Answer: If in a prior study, a sample of 200 people showed that 40 traveled overseas last year, then n= 385

If no estimate of the sample proportion is available , then n= 601

Explanation:

Let p be the prior population proportion of people who traveled overseas last year.

If p is known, then required sample size =
`n=p(1-p)((z^*)/(E))^2`

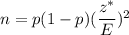
z-value for 95% confidence = 1.96

E = 0.04 (given)

`p=(40)/(200)=0.2`

`n=0.2(1-0.2)((1.96)/(0.04))^2=384.16\approx385`

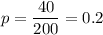
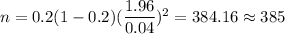
Required sample size = 385

If p is unknown, then required sample size =
`n=0.25((z^*)/(E))^2`

, where E = Margin of error , z* =critical z-value.

z-value for 95% confidence = 1.96

E = 0.04 (given)

So,
`n=0.25((1.96)/(0.04))^2=600.25\approx601`

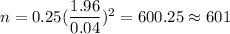
Required sample size = 601.