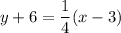Point-Slope Form
This is one way we can represent a linear equation:

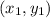 is a point that falls on the line
is a point that falls on the line
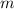 is the slope
is the slope
Solving the Question
We're given:
- Line contains
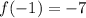 and
and
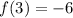
These functions give us information on two points, as they are represented as
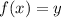 :
:
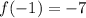 ⇒ (-1, -7)
⇒ (-1, -7)
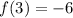 ⇒ (3,-6)
⇒ (3,-6)
First, solve for the slope:
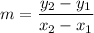
⇒ Plug in the two points:
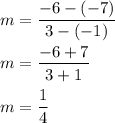
⇒ Plug this into
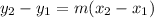 :
:
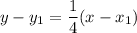
Now, there are two ways we can write this equation, as we are given two points:
(-1, -7)
⇒
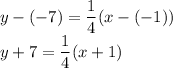
(3,-6)
⇒
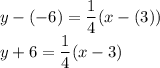
Answer
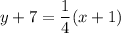 or
or