Answer:
6 seconds
Explanation:
Given function:
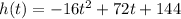
where:
- h is the height of the rocket.
- t is the time (in seconds) after launch.
To find how long the rocket is in the air, find the positive value of t when h(t)=0.
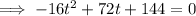
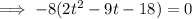
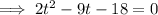


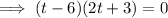
Apply the zero-product property:
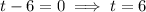
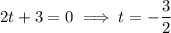
Therefore, as t > 0, the rocket is in the air for 6 seconds.