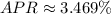Answer:
Compounded Semiannually:
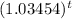 and APR = 3.454%
and APR = 3.454%
Compounded Quarterly:
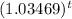 and APR = 3.469%
and APR = 3.469%
Explanation:
Compound Interest Formula:
The Compound Interest Formula is as follows:
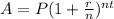 , which can also be written as:
, which can also be written as:
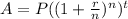 , using properties of exponents. This is crucial since we want one value inside the parenthesis to calculate the APR (Annual Percentage Rate). Since we want the APR, the only thing we really care about is the
, using properties of exponents. This is crucial since we want one value inside the parenthesis to calculate the APR (Annual Percentage Rate). Since we want the APR, the only thing we really care about is the
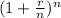 , but this is going to be our APR + 1.
, but this is going to be our APR + 1.
In the question, it's formatted as:
 , and this inside part is going to be our b, so:
, and this inside part is going to be our b, so:
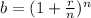 , and to calculate the APR we simply subtract 1.
, and to calculate the APR we simply subtract 1.
Calculating APR:
Compounded semiannually means the interest is compounded twice a year, so n = 2. We are also given the interest to be 3.425% which in decimal form is 0.03425
Plugging this into the formula stated above we get:
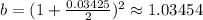
So we have the form:
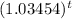
With our APR simply being the base - 1:
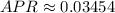
We multiply this by 100 to get it in percentage form:
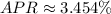
Compounded quarterly means the interest is compounded four times a year, so n = 4. Plugging in known values we get:

So we have the form:
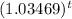
With our APR simply being the base - 1

Multiply this by 100 to get it in percentage form: