Question

Write a quadratic function with the given zero. 3 + i

Answer 1

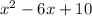`x^2 - 6x + 10` or in general:
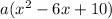`a(x^2 - 6x + 10)` where "a" is any constant real number except zero.

Explanation:

Complex Conjugate Root Theorem:

If we're given a complex root of a polynomial to be:
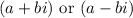`(a+bi)\text{ or }(a-bi)`, then we know that its conjugate is also a root of the polynomial:
`(a-bi)\text{ or }(a+bi)`.

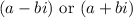So since we're given the root:
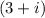`(3+i)`, then we know that its conjugate:
`(3-i)` is also a root. Thus we have two roots so far.

Fundamental Theorem of Algebra:

The Fundamental Theorem of Algebra simply states that any polynomial, with degree "n", will have "n" roots, which can consist of both real and imaginary solutions.

So let's say I have a polynomial:
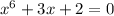`x^6+3x+2=0`, this has 6 roots, according to the Fundamental Theorem of Algebra, since the degree of the polynomial is 6 (remember the degree is simply the variable with the highest degree)

Since we already have two roots, and a quadratic function has a degree of two, we know that these are all the roots the quadratic has, since the Fundamental Theorem of Algebra states that a quadratic will only have 2 roots.

Factored Form:

We can generally express any polynomial in factored form, that is:
`a(x-b)(x-c)(x-d)...=y`

where "b", "c", and "d", and so on... are zeros of the function. This aligns with the behavior of zeros, since if we plug any of them into the function, then one of the factors will become zero, and since zero times anything is zero, well the entire thing is zero.

For example if I plug in "b", which is zero we get:
`a(b-b)(b-c)(b-d)...=y\implies a(0)(b-c)(b-d)=y\implies 0=y`

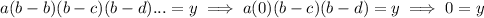
this is since plugging in zero, makes the factor:
`x-b` equal to zero, making the entire thing zero.

One last thing to mention is the "a" value in front which just generally determines the stretch/compression of the polynomial.

So with this information, we can write a polynomial:

`a(x-(3+i))(x-(3-i))`

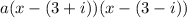
From here let's distribute the negative sign:

`a(x-3-i)(x-3+i)`

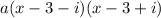
Now this may look a bit tough to distribute, but you may notice a pattern here, we have a difference of squares. It may not be obvious, but if we make one substitution, let's say:
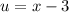`u=x-3`, then we get the equation

`a(u-i)(u+i)`

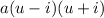
The difference of squares is expressed as:
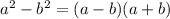`a^2 - b^2 = (a-b)(a+b)`, so our expression will expand out into:

`a(u^2 - i^2)`

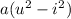
The substitution was just to make things a bit more clear, but let's just substitute x-3 back into the equation.

`a((x-3)^2 - i^2)`

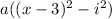
From here, we know that i^2 is simply -1, since:
`√(-1) = i, \text{ so }i^2 = -1`

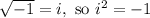
We can also easily expand out the polynomial using FOIL

`a((x^2 - 6x + 9) -(-1))\\a(x^2 - 6x + 9 + 1)\\a(x^2 - 6x + 10)`

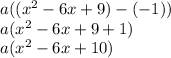
You may notice the "a value, and that's just a constant, which determines the stretch/compression of the polynomial, and can be any real number, except for zero since that will make the entire thing zero regardless of what x is. For the sake of simplicity, let's just write this to be 1.