Question

Question 4

The weights for 12-month-old baby boys are normally distributed with a mean of 22.5 pounds and a standard deviation of 2.2 pounds.

Find the percentage to the nearest tenth of 12-month-old baby boys who weigh between 19.7 and 24.4 pounds.

ANSWER -

Answer 1

70.5%

Explanation:

If a continuous random variable X is normally distributed with mean μ and variance σ², it is written as:

`\large\boxed{X \sim\text{N}(\mu,\sigma^2)}`

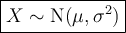
Given:

• Mean μ = 22.5
• Standard deviation σ = 2.2

Therefore, if the weights of the 12-month-old baby boys are normally distributed:

`\boxed{X \sim\text{N} \left(22.5,2.2^2 \right)}`

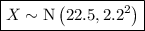
where X is the weight of the baby boy.

To find the percentage to the nearest tenth of 12-month-old baby boys who weigh between 19.7 and 24.4 pounds find P(19.7 ≤ X ≤ 24.4).

Calculator input for "normal cumulative distribution function (cdf)":

• Upper bound: x = 19.7
• Lower bound: x = 24.4
• σ = 2.2
• μ = 22.5

`\implies \text{P}(19.7 \leq X \leq 24.4)=0.704548741`

`\implies \text{P}(19.7 \leq X \leq 24.4)=70.5\%`

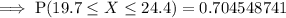
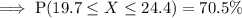
Therefore, the percentage of 12-month-old baby boys who weigh between 19.7 and 24.4 pounds is 70.5% (nearest tenth).