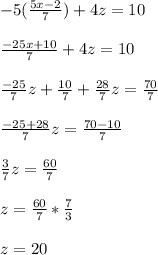Answer:
z = 20
Explanation:
Elimination Method:
We can use the elimination method in a systems of 3 equations, just as we did when we were solving systems of 2 equations. While the method we apply it is the same, we have to apply it multiple times as elimination gets rid of one variable (usually) and since we're dealing with 3 variables, that still leaves us with 2 variables and we need to cancel once more.
Applying Elimination Method:
We want to develop two linear equations, by applying elimination twice to each equation at least once, and then from there we can apply elimination once more.
Since we're solving for "z", we don't want to immediately cancel it out. So let's use the following two equations:
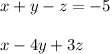
Let's cancel out the "x", by manipulating one equation to be -x. We can do this by multiplying one equation by -1, but remember we have to apply this to both sides of the equation. Let's do it to the top one (you could also do it to the bottom one)
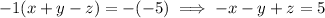
So now let's add the two equations:
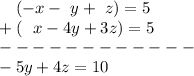
Now let's apply the same thing, but to the middle and bottom equation. Since they don't have the same absolute value coefficients (ignoring the sign) we need to multiple one by a value other than just negative one. So let's multiply the bottom equation by -2 so that the bottom will have a -2x which will cancel when adding it to 2x
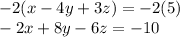
Now let's add the equations:
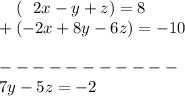
So now we have the two equations:
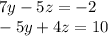
From here we can apply any method we want, from here I'll use substitution. Since we want to get rid of the "y", let's solve for "y" in terms of z, so once we substitute we have no "y" terms left.
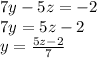
Now let's plug this into the second two-variable equation we made.