Question

The perimeter of a triangle is 3x² + 6x - 9. If one side length is x² + 2x - 1 and the

other is x² + x - 5, what is the length of the 3rd side?

Answer 1

x^2+3x-3

Explanation:

(x^2+2x-1)+(x^2+x-5)

2x^2+3x-6

(3x^2+6x-9)-(2x^2+3x-6)

x^2+3x-3

hopes this helps

Answer 2

`x^2 + 3x - 3`

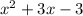
Explanation:

The perimeter of a triangle, can be calculated as, the sum of the sides.

So let's first assume the third side is a polynomial, and more specifically, a quadratic in the form:
`ax^2+bx+c`. This assumption is denoted from the fact that the perimeter only has terms up to the degree of 2, also known as x squared. The answer is also a quadratic, so it isn't an unreasonable assumption that if we add two quadratics (the ones given), and add one more quadratic, we should still have quadratic.

So, the sum of the three sides can be expressed as:
`(x^2 + 2x - 1) + (x^2 + x - 5) + (ax^2 + bx + c)`

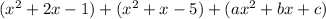
We can combine like terms to get:

`(x^2+x^2+ax^2)+(2x+x+bx)+(-1-5+c)`

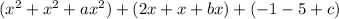
Now from here, we can combine like terms (add coefficients):

`(2+a)x^2 + (3+b)x + (-6+c)`

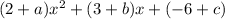
From here, we simply set this equal to the given perimeter of:
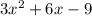`3x^2 + 6x-9`, which gives us the equation:

`(2+a)x^2 + (3+b)x+(-6+c) = 3x^2 + 6x - 9`

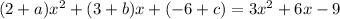
Now from here, the coefficients need to correspond for both quadratics to be equal to each other, so that means that the following must be true:

`(2+a)=3\implies a = 1\\(3 + b) = 6\implies b = 3\\(-6 +c) = -9 \implies c = -3`

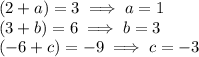
We now plug this into the quadratic standard form to get:

`x^2 + 3x - 3`

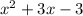
Which is our third side!