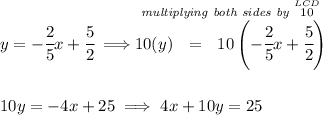Question

Which is the result when the equation y = -2/5x + 5/2 is converted to
standard form?

Answer 1

standard form for a linear equation means

• all coefficients must be integers, no fractions

• only the constant on the right-hand-side

• all variables on the left-hand-side, sorted

• "x" must not have a negative coefficient

to do away with the denominators, we can just use the LCD of all denominators and multiply both sides by it hmm, in this case is 10, the LCD of 5 and 2, so we'll use that.

`y=-\cfrac{2}{5}x+\cfrac{5}{2}\implies \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{10}}{10(y)~~ = ~~10\left( -\cfrac{2}{5}x+\cfrac{5}{2} \right)} \\\\\\ 10y=-4x+25 \implies 4x+10y=25`

Answer 2

`4x+10y-25=0`

Explanation:

`y=-(2)/(5) x+(5)/(2)`

Multiply by 10 on both sides,

`10y=-4x+25\\`

so
`4x+10y-25=0`